吟詠と音楽
音の正体 音の種類 倍音の不思議 音律 共鳴
| 音 律 | |||||||||||||||||||||||||||||||||
| 十二平均律 | |||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||
| 調子笛には12種類の高さが備わっているものがあります。 洋楽ではAからG#まで、吟詠では1本から12本の高さが得られます。 現在、一般的に使用されている調子笛やチューナーは、十二平均律という音律になっています。 |
|||||||||||||||||||||||||||||||||
| Aの音(1本)は440Hz、1オクターブ高いA(13本)は440Hzの2倍の周波数になるのですが、1オクターブを均等に12の半音で割って得た音律が十二平均律です。 十二平均律が西洋で普及したのは19世紀頃からで、現在では世界的標準音律として定着しています。 十二平均律が定着する以前、いくつもの音律が考案され使用されてきましたが、それぞれに長所と短所がありました。 |
|||||||||||||||||||||||||||||||||
| ピタゴラス音律 | |||||||||||||||||||||||||||||||||
| 西洋では十二平均律に至るまでに、音律は幾種類かの変遷を経てきましたが、すべての音律の元になったのは、古代ギリシャのピタゴラス音律でした。 |
|||||||||||||||||||||||||||||||||
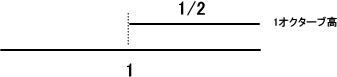 弦あるいは管の長さを半分(1/2)にすると1オクターブ高い音が得られます。 |
|||||||||||||||||||||||||||||||||
 長さを2/3にすると完全5度(7律)高い音が得られます。元の長さをドとすれば、ソが得られることになります。 |
|||||||||||||||||||||||||||||||||
| 完全5度の原理 | |||||||||||||||||||||||||||||||||
| 完全5度の音程は、おそらく原始の頃からすべての民族が使用していた音程と思われます。人類が早くから倍音の原理を経験的に見つけていたとも言えるでしょう。 ピタゴラス音律で得られる完全5度は、元の1.5倍の振動数であり、倍音とも一致するので、大変きれいな5度になります。 (これに対して、平均律で得られる完全5度は、若干狭い5度になり、響きの透明度としては劣りますが、その他の多くの音楽的利点があるため、世界的に普及したのです。 |
|||||||||||||||||||||||||||||||||
| ピタゴラスの方法を繰り返すと、 ド⇒ソ⇒レ⇒ラ⇒ミ という、民族音楽の基本となる五音階が出来上がります。 更に、繰り返すと、 ド⇒ソ⇒レ⇒ラ⇒ミ⇒シ⇒ファ#⇒ド#⇒ソ#⇒レ#⇒ラ#⇒ミ#(ファ)⇒ド と、1オクターブ中に12種類の音高が得られます。 ただ、 ピタゴラス音律では、最後に得られるドが元のドの高さに一致しないという弱点がありました。 この弱点を補うには、オクターブの間の他の音程にしわよせをさせる必要がでてきます。 結果的に、ピアゴラス音律で調律されたピアノなど鍵盤楽器は、調律された調しか演奏できないことになり、転調や移調といった音楽的発展には貢献できない音律とならざるを得ませんでした。 |
|||||||||||||||||||||||||||||||||
| 純正律 | |||||||||||||||||||||||||||||||||
| 和音音楽の時代になると、ピタゴラス音律で得たドミソなど、三和音が濁る(ミの音高の為)という弱点も指摘されることとなりました。 純正律は、ピアゴラス音律の和音の弱点を改良しようと考案された音律です。 ただ、純正律では主要三和音の響きはきれいですが、他の和音で濁る欠点があり、更にピアゴラス音律と同様に、純正律で調律された楽器は、その調専用で、移調や転調ができないという不都合もありました。 |
|||||||||||||||||||||||||||||||||
| 中全律 | |||||||||||||||||||||||||||||||||
| すべての三和音を平均的にきれいに響かせようとして考案されましたが、他の要素にしわ寄せが発生するという悪循環から脱することはできませんでした。 | |||||||||||||||||||||||||||||||||
| 平均律 | |||||||||||||||||||||||||||||||||
| 器楽音楽が発展するに伴い、移調や転調など、即座にに対応できる調律が必要になってきた時代に、1オクターブを12等分する音律が考案されました。バッハによる「平均律クラヴィーア曲集」が、この音律の普及に貢献したことは有名です。 | |||||||||||||||||||||||||||||||||
| 音楽芸術をあらゆる要素で総合的に高める為には、何か一つの要素の完璧を求めることより、すべての要素に対して平均的な妥協を見出すことが最善の方法となったのです。 | |||||||||||||||||||||||||||||||||
| 音律の比較 | |||||||||||||||||||||||||||||||||
| A調(イ長調)のドミソを、ピタゴラス音律・純正律・十二平均律を周波数で比較すると次のようになります。 | |||||||||||||||||||||||||||||||||
長所:一部を除いてほぼすべてが 完全5度なので単旋律は美しい。ミの音が純正律や平均律よりも高いので、長調と短調の差がより顕著に聞こえる。 短所:三和音が濁る。移調・転調が困難。 |
長所:主要三和音が美しい。 短所:他の和音で響きの悪い和音ができる。音階が不自然になる。移調・転調が困難。 |
||||||||||||||||||||||||||||||||
長所:移調・転調が自在。 短所:和音がやや濁る。 |
|||||||||||||||||||||||||||||||||
| 今日の現実的音律 | |||||||||||||||||||||||||||||||||
| 近代以降の音楽の現場では、十二平均律に従っているのですが、音楽の演奏が寸分の狂いもない平均律で演奏されているわけではありません。 電子楽器のようにピッチ変動がない楽器はともかく、人間が歌ったり演奏したりする際には、音楽の流れの中で、自然に瞬間的に平均律から外れることはあります。外れるといっても、ピッチがずれるようなものではなく、たとえばフレーズの中のある音が平均律より1〜4Hz程度低くあるいは高く演奏した・・・というようなものです。 また、装飾的にピッチの不鮮明な音を用いることもありますし、つまりは、音楽は生き物であって、すべてを数量的に固定できるものではないということです。 |
|||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||